 pROC 1.19.0
pROC 1.19.0
pROC version 1.19.0 was just released and will be available on CRAN very soon.
Besides minor changes and fixes in the coords and ci.coords functions,
the main updates in this version focus on the core of the package, aiming to make it more modern, efficient, and easier
to maintain. Several features that were difficult to maintain have been deprecated.
- The dependency on the retired plyr package has been removed (thanks to Michael Chirico for his contributions).
Unfortunately, as a side effect, progress bars and parallel processing have been removed.
Trying to set the
progressandparallelarguments will now trigger a warning, and the arguments will be ignored. - As a followup from the changes to the output of the
coordsfunction in version 1.16.0, thetranspose,as.list,as.matrixanddroparguments have been deprecated. Thecoordsfunction currently has multiple exit points, depending on arguments and inputs, and can return retults in mutliple formats. This makes it difficult to use and to maintain. Going forward,coordswill only retrun data in a single, tidydata.frameformat, compatible following modern R coding practices. For compatibility reasons, deprecated arguments are still available, but setting them to non default values will trigger warnings. They will be removed in a future release. If your code still uses these arguments, please update it accordingly. - Finally, following years of performance improvements, an in an effort to simplify the codebase, all ROC computation
algorithms other than 2 have been removed as they no longer provided meaningful performance advantages. The
algorithmargument torochas been deprecated. Setting it to a non-default value has no effect and triggers a warning. Thefun.sespvalue ofrocobjects is also deprecated. Calling it triggers a warning. Both will be removed in a future release of pROC.
Here is the full changelog:
ci.coordscan now take the sameinputvalues ascoords(issue #90)ci.coordscan beplotted- Added "lr_pos" and "lr_neg" to
coords(issue #102) coordswith partial.auc now interpolates bounds when needed- Added
ignore.partial.aucargument tocoords - Deprecated
transpose,as.list,as.matrixanddropincoords - Deprecated the
algorithmargument torocandfun.sespvalue - Deprecated the
progressandparallelargument for bootstrap operations. - Removed dependencies on doParallel and retired package plyr (thanks to Michael Chirico, pr #134, #135, #136, #137, #138, #139 and #140).
You can update your installation by simply typing:
install.packages("pROC")
Update: pROC 1.19.0 was rejected from CRAN. A patch revision 1.19.0.1 was created to workaround an issue with a reverse dependency but provides no meaningful change:
- Move
fun.sespdefinition to work around LudvigOlsen/cvms#44.
Xavier Robin
Published Wednesday, July 30, 2025 18:56 CEST
Permalink: /blog/2025/07/30/proc-1.19.0
Tags:
pROC
Comments: 0
 pROC 1.18.5
pROC 1.18.5
pROC 1.18.5 is now available on CRAN. It's a minor bugfix release:
- Fixed formula input when given as variable and combined with
with(issue #111) - Fixed formula containing variables with spaces (issue #120)
- Fixed broken grouping when
colourargument was given inggroc(issue #121)
You can update your installation by simply typing:
install.packages("pROC")Xavier Robin
Published Thursday, November 2, 2023 17:01 CET
Permalink: /blog/2023/11/02/proc-1.18.5
Tags:
pROC
Comments: 0
 Deep Learning of MNIST handwritten digits
Deep Learning of MNIST handwritten digits
In this document I am going create a video showing the training of the inner-most layer of Deep Belief Network (DBN) using the MNIST dataset of handwritten digits. I will use our DeepLearning R package that implements flexible DBN architectures with an object-oriented interface.
MNIST
The MNIST dataset is a database of handwritten digits with 60,000 training images and 10,000 testing images. You can learn everything about it on Wikipedia. In short, it is the go-to dataset to train and test handwritten digit recognition machine learning algorithms.
I made an R package for easy access, named mnist. The easiest way to install it is with devtools. If you don't have it already, let's first install devtools:
if (!require("devtools")) {install.packages("devtools")}
Now we can install mnist:
devtools::install_github("xrobin/mnist")
PCA
In order to see what the dataset looks like, let's use PCA to reduce it to two dimensions.
pca <- prcomp(mnist$train$x) plot.mnist( prediction = predict(pca, mnist$test$x), reconstruction = tcrossprod( predict(pca, mnist$test$x)[,1:2], pca$rotation[,1:2]), highlight.digits = c(72, 3, 83, 91, 6688, 7860, 92, 1, 180, 13))
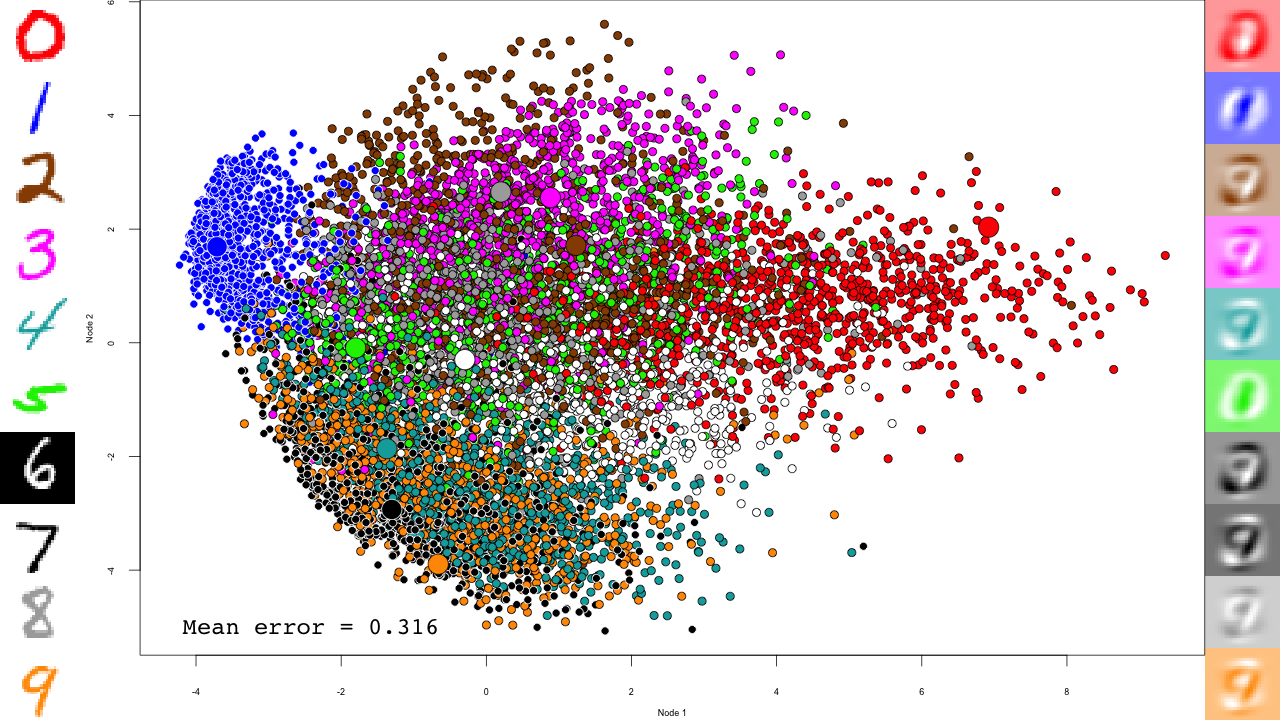
Let's take a minute to describe this plot. The central scatterplot shows first two components of the PCA of all digits in the test set. On the left hand side, I picked 10 representative digits from the test set to highlight, which are shown as larger circles in the central scatterplot. On the left are the "reconstructed digits", which were reconstructed from the two first dimensions of the PCA. While we can see some digit-like structures, it is basically impossible to recognize them. We can see some separation of the digits in the 2D space as well, but it is pretty weak and some pairs cannot be distinguished at all (like 4 and 9). Of course the reconstructions would look much better had we kept all PCA dimensions, but so much for dimensionality reduction.
Deep Learning
Now let's see if we can do better with Deep Learning. We'll use a classical Deep Belief Network (DBN), based on Restricted Boltzmann Machines (RBM) similar to what Hinton described back in 2006 (Hinton & Salakhutdinov, 2006). The training happens in two steps: a pre-training step with contrastive divergence stochastic gradient descent brings the network to a reasonable starting point for a more conventional conjugate gradient optimization (hereafter referred to as fine-tuning).
I implemented this algorithm with a few modifications in an R package which is available on GitHub. The core of the processing is done in C++ with RcppEigen (Bates & Eddelbuettel, 2013) for higher speed. Using devtools again:
devtools::install_github("xrobin/DeepLearning")
We will use this code to train a 5 layers deep network, that reduces the digits to an abstract, 2D representation. By looking at this last layer throughout the training process we can start to understand how the network learns to recognize digits. Let's start by loading the required packages and the MNIST dataset, and create the DBN.
library(DeepLearning) library(mnist) data(mnist) dbn <- DeepBeliefNet(Layers(c(784, 1000, 500, 250, 2), input = "continuous", output = "gaussian"), initialize = "0")
We just created the 5-layers DBN, with continuous, 784 nodes input (the digit image pixels), and a 2 nodes, gaussian output. It is initialized with 0, but we could have left out the initialize to start from a random initilization (Bengio et al., 2007). Before we go, let's define a few useful variables:
output.folder <- "video" # Where to save the output maxiters.pretrain <- 1e6 # Number of pre-training iterations maxiters.train <- 10000 # Number of fine-tuning iterations run.training <- run.images <- TRUE # Turn any of these off # Which digits to highlight and reconstruct highlight.digits = c(72, 3, 83, 91, 6688, 7860, 92, 1, 180, 13)
We'll also need the following function to show the elapsed time:
format.timediff <- function(start.time) {
diff = as.numeric(difftime(Sys.time(), start.time, units="mins"))
hr <- diff%/%60
min <- floor(diff - hr * 60)
sec <- round(diff%%1 * 60,digits=2)
return(paste(hr,min,sec,sep=':'))
}
Pre-training
Initially, the network is a stack of RBMs that we need to pre-train one by one. Hinton & Salakhutdinov (2006) showed that this step is critical to train deep networks. We will use 1000000 iterations (maxiters.pretrain) of contrastive divergence, which takes a couple of days on a modern CPU. Let's start with the first three RBMs:
First three RBMs
if (run.training) {
sprintf.fmt.iter <- sprintf("%%0%dd", nchar(sprintf("%d", maxiters.pretrain)))
mnist.data.layer <- mnist
for (i in 1:3) {
We define a diag function that will simply print where we are in the training. Because this function will be called a million times (maxiters.pretrain), we can use rate = "accelerate" to slow down the printing over time and save a few CPU cycles.
diag <- list(rate = "accelerate", data = NULL, f = function(rbm, batch, data, iter, batchsize, maxiters, layer) {
print(sprintf("%s[%s/%s] in %s", layer, iter, maxiters, format.timediff(start.time)))
})
We can get the current RBM, and we will work on it directly. Let's save it for good measure, as well as the current time for the progress function:
rbm <- dbn[[i]]
save(rbm, file = file.path(output.folder, sprintf("rbm-%s-%s.RData", i, "initial")))
start.time <- Sys.time()
Now we can start the actual pre-training:
rbm <- pretrain(rbm, mnist.data.layer$train$x, penalization = "l2", lambda=0.0002, momentum = c(0.5, 0.9), epsilon=c(.1, .1, .1, .001)[i], batchsize = 100, maxiters=maxiters.pretrain, continue.function = continue.function.always, diag = diag)
This can take some time, especially for the first layers which are larger. Once it is done, we predict the data through this RBM for the next layer and save the results:
mnist.data.layer$train$x <- predict(rbm, mnist.data.layer$train$x)
mnist.data.layer$test$x <- predict(rbm, mnist.data.layer$test$x)
save(rbm, file = file.path(output.folder, sprintf("rbm-%s-%s.RData", i, "final")))
dbn[[i]] <- rbm
}
Last RBM
This is very similar to the previous three, but note that we save the RBM within the diag function. We could generate the plot directly, but it is easier to do it later once we have some idea about the final axis we will need. Please note the rate = "accelerate" here. You probably don't want to save a million RBM objects on your hard drive, both for speed and space reasons.
rbm <- dbn[[4]]
print(head(rbm$b))
diag <- list(rate = "accelerate", data = NULL, f = function(rbm, batch, data, iter, batchsize, maxiters, layer) {
save(rbm, file = file.path(output.folder, sprintf("rbm-4-%s.RData", sprintf(sprintf.fmt.iter, iter))))
print(sprintf("%s[%s/%s] in %s", layer, iter, maxiters, format.timediff(start.time)))
})
save(rbm, file = file.path(output.folder, sprintf("rbm-%s-%s.RData", 4, "initial")))
start.time <- Sys.time()
rbm <- pretrain(rbm, mnist.data.layer$train$x, penalization = "l2", lambda=0.0002,
epsilon=.001, batchsize = 100, maxiters=maxiters.pretrain,
continue.function = continue.function.always, diag = diag)
save(rbm, file = file.path(output.folder, sprintf("rbm-4-%s.RData", "final")))
dbn[[4]] <- rbm
If we were not querying the last layer, we could have pre-trained the entire network at once with the following call:
dbn <- pretrain(dbn, mnist.data.layer$train$x, penalization = "l2", lambda=0.0002, momentum = c(0.5, 0.9), epsilon=c(.1, .1, .1, .001), batchsize = 100, maxiters=maxiters.pretrain, continue.function = continue.function.always)
Pre-training parameters
Pre-training RBMs is quite sensitive to the use of proper parameters. With improper parameters, the network can quickly go crazy and start to generate infinite values. If that happens to you, you should try to tune one of the following parameters:
penalization: this is the penalty of introducing or increasing the value of a weight. We used L2 regularization, but"l1"is available if a sparser weight matrix is needed.lambda: the regularization rate. In our experience 0.0002 works fine with the MNIST and other datasets of similar sizes such as cellular imaging data. Too small or large values will result in over- or under-fitted networks, respectively.momentum: helps avoiding oscillatory behaviors, where the network oscillate between iterations. Allowed values can range from 0 (no momentum) to 1 (full momentum = no training). Here we used an increasing gradient of momentum which starts at 0.5 and increases linearly to 0.9, in order to stabilize the final network without compromising early training steps.epsilon: the learning rate. Typically, 0.1 works well with binary and continuous output layers, and must be decreased to around 0.001 for gaussian outputs. Too large values will drive the network to generate infinities, while too small ones will slow down the training.batchsize: larger batch sizes will result in smoother but slower training. Small batch sizes will make the training "jumpy", which can be compensated by lower learning rates (epsilon) or increased momentum.
Fine-tuning
This is where the real training happens. We use conjugate gradients to find the optimal solution. Again, the diag function saves the DBN. This time we use rate = "each" to save every step of the training. First we have way fewer steps, but also the training itself happen at a much more stable speed than in the pre-training, where things slow down dramatically.
sprintf.fmt.iter <- sprintf("%%0%dd", nchar(sprintf("%d", maxiters.train)))
diag <- list(rate = "each", data = NULL, f = function(dbn, batch, data, iter, batchsize, maxiters) {
save(dbn, file = file.path(output.folder, sprintf("dbn-finetune-%s.RData", sprintf(sprintf.fmt.iter, iter))))
print(sprintf("[%s/%s] in %s", iter, maxiters, format.timediff(start.time)))
})
save(dbn, file = file.path(output.folder, sprintf("dbn-finetune-%s.RData", "initial")))
start.time <- Sys.time()
dbn <- train(unroll(dbn), mnist$train$x, batchsize = 100, maxiters=maxiters.train,
continue.function = continue.function.always, diag = diag)
save(dbn, file = file.path(output.folder, sprintf("dbn-finetune-%s.RData", "final")))
}
And that's it, our DBN is now fully trained!
Generating the images
Now we need to read in the saved network states again, pass the data through the network (predict) and save this in HD-sized PNG file.
The first three RBMs are only loaded into the DBN
if (run.images) {
for (i in 1:3) {
load(file.path(output.folder, sprintf("rbm-%d-final.RData", i)))
dbn[[i]] <- rbm
}
The last RBM is where interesting things happen.
for (file in list.files(output.folder, pattern = "rbm-4-.+\\.RData", full.names = TRUE)) {
print(file)
load(file)
dbn[[4]] <- rbm
iter <- stringr::str_match(file, "rbm-4-(.+)\\.RData")[,2]
We now predict and reconstruct the data, and calculate the mean reconstruction error:
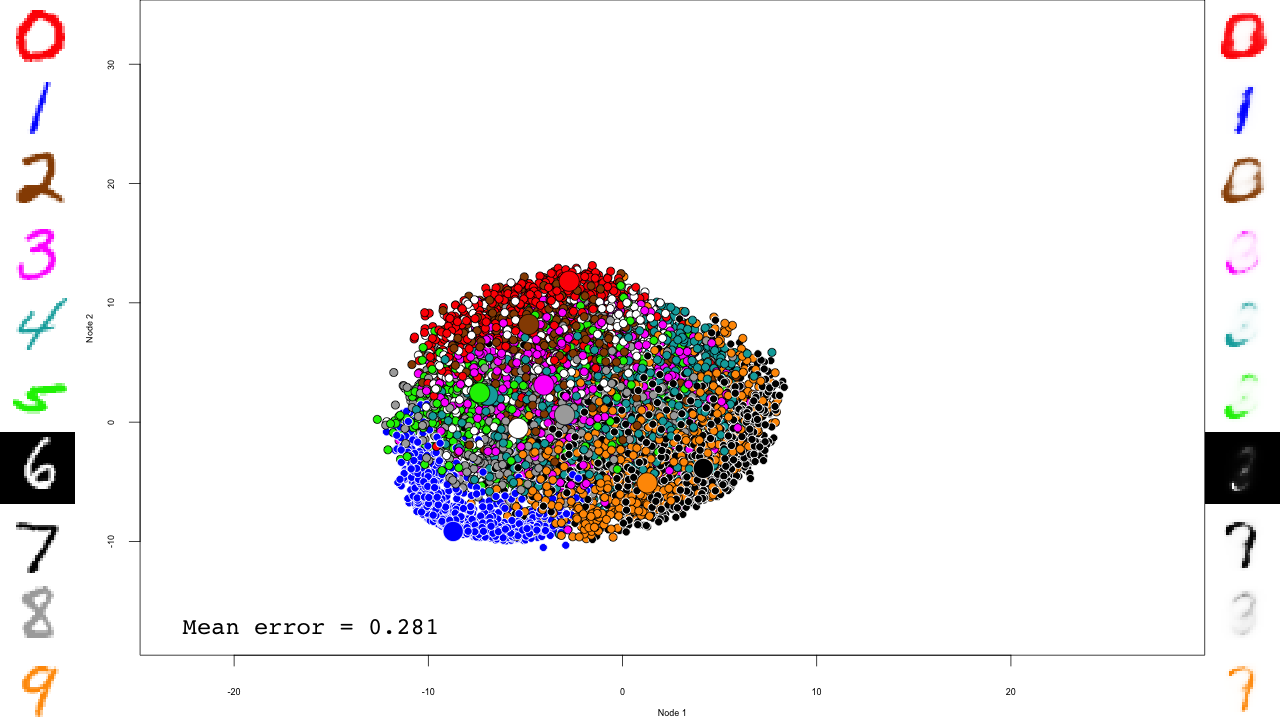
predictions <- predict(dbn, mnist$test$x) reconstructions <- reconstruct(dbn, mnist$test$x) iteration.error <- errorSum(dbn, mnist$test$x) / nrow(mnist$test$x)
Now the actual plotting. Here I selected xlim and ylim values that worked well for my training run, but your mileage may vary.
png(sub(".RData", ".png", file), width = 1280, height = 720) # hd output
plot.mnist(model = dbn, x = mnist$test$x, label = mnist$test$y+1, predictions = predictions, reconstructions = reconstructions,
ncol = 16, highlight.digits = highlight.digits,
xlim = c(-12.625948, 8.329168), ylim = c(-10.50657, 13.12654))
par(family="mono")
legend("bottomleft", legend = sprintf("Mean error = %.3f", iteration.error), bty="n", cex=3)
legend("bottomright", legend = sprintf("Iteration = %s", iter), bty="n", cex=3)
dev.off()
}
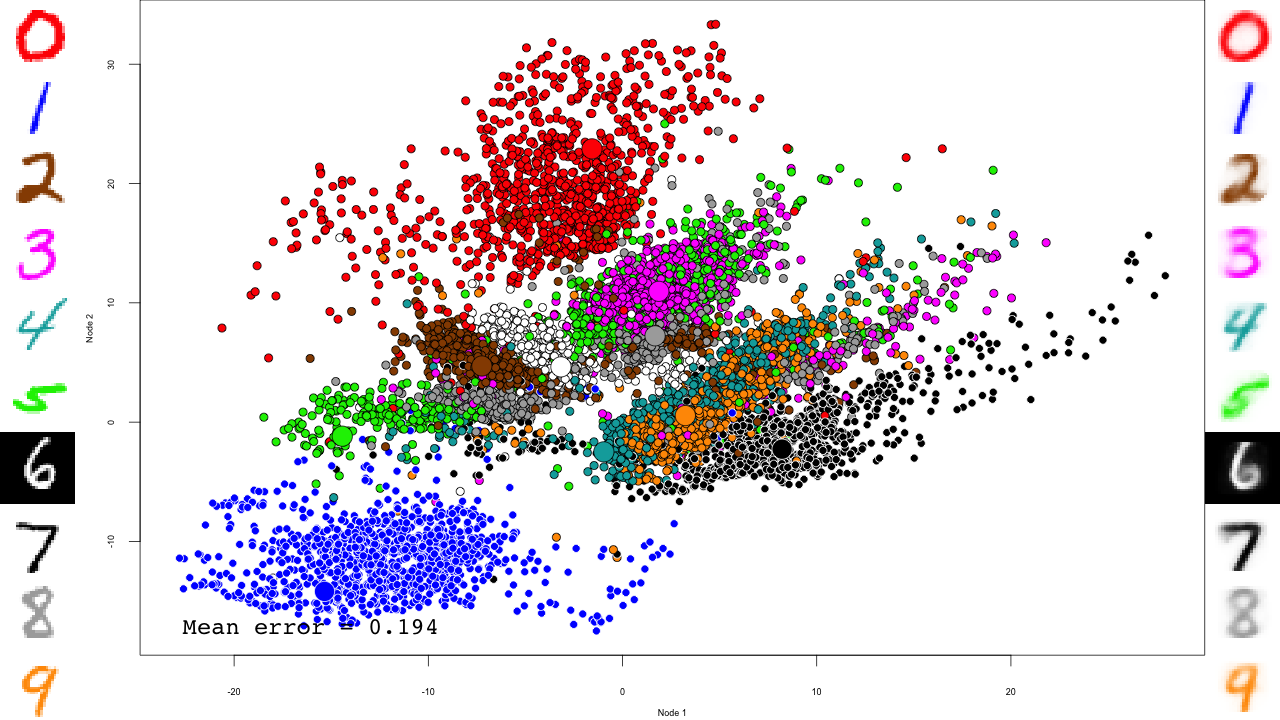
We do the same with the fine-tuning:
for (file in list.files(output.folder, pattern = "dbn-finetune-.+\\.RData", full.names = TRUE)) {
print(file)
load(file)
iter <- stringr::str_match(file, "dbn-finetune-(.+)\\.RData")[,2]
predictions <- predict(dbn, mnist$test$x)
reconstructions <- reconstruct(dbn, mnist$test$x)
iteration.error <- errorSum(dbn, mnist$test$x) / nrow(mnist$test$x)
png(sub(".RData", ".png", file), width = 1280, height = 720) # hd output
plot.mnist(model = dbn, x = mnist$test$x, label = mnist$test$y+1, predictions = predictions, reconstructions = reconstructions,
ncol = 16, highlight.digits = highlight.digits,
xlim = c(-22.81098, 27.94829), ylim = c(-17.49874, 33.34688))
par(family="mono")
legend("bottomleft", legend = sprintf("Mean error = %.3f", iteration.error), bty="n", cex=3)
legend("bottomright", legend = sprintf("Iteration = %s", iter), bty="n", cex=3)
dev.off()
}
}
The video
I simply used ffmpeg to convert the PNG files to a video:
cd video ffmpeg -pattern_type glob -i "rbm-4-*.png" -b:v 10000000 -y ../rbm-4.mp4 ffmpeg -pattern_type glob -i "dbn-finetune-*.png" -b:v 10000000 -y ../dbn-finetune.mp4
And that's it! Notice how the pre-training only brings the network to a state similar to that of a PCA, and the fine-tuning actually does the separation, and how it really makes the reconstructions accurate.
Application
We used this code to analyze changes in cell morphology upon drug resistance in cancer. With a 27-dimension space, we could describe all of the observed cell morphologies and predict whether a cell was resistant to ErbB-family drugs with an accuracy of 74%. The paper is available in Open Access in Cell Reports, DOI 10.1016/j.celrep.2020.108657.
Concluding remarks
In this document I described how to build and train a DBN with the DeepLearning package. I also showed how to query the internal layer, and use the generative properties to follow the training of the network on handwritten digits.
DBNs have the advantage over Convolutional Networks (CN) that they are fully generative, at least during the pre-training. They are therefore easier to query and interpret as we have demonstrated here. However keep in mind that CNs have demonstrated higher accuracies on computer vision tasks, such as the MNIST dataset.
Additional algorithmic details are available in the doc folder of the DeepLearning package.
References
- Our paper, 2021
- Longden J., Robin X., Engel M., et al. Deep neural networks identify signaling mechanisms of ErbB-family drug resistance from a continuous cell morphology space. Cell Reports, 2021;34(3):108657.
- Bates & Eddelbuettel, 2013
- Bates D, Eddelbuettel D. Fast and Elegant Numerical Linear Algebra Using the RcppEigen Package. Journal of Statistical Software, 2013;52(5):1–24.
- Bengio et al., 2007
- Bengio Y, Lamblin P, Popovici D, Larochelle H. Greedy layer-wise training of deep networks. Advances in neural information processing systems. 2007;19:153–60.
- Hinton & Salakhutdinov, 2006
- Hinton GE, Salakhutdinov RR. Reducing the Dimensionality of Data with Neural Networks. Science. 2006;313(5786):504–7.
Downloads
Xavier Robin
Published Saturday, June 11, 2022 16:39 CEST
Permalink: /blog/2022/06/11/deep-learning-of-mnist-handwritten-digits
Tags:
Programming
Comments: 0
 pROC 1.18.0
pROC 1.18.0
pROC version 1.18.0 is now available on CRAN now. Only a few changes were implemented in this release:
- Add CI of the estimate for
roc.test(DeLong, paired only for now) (code contributed by Zane Billings) (issue #95). - Fix documentation and alternative hypothesis for Venkatraman test (issue #92).
You can update your installation by simply typing:
install.packages("pROC")Xavier Robin
Published Monday, September 6, 2021 18:34 CEST
Permalink: /blog/2021/09/06/proc-1.18.0
Tags:
pROC
Comments: 2
 pROC 1.17.0.1
pROC 1.17.0.1
pROC version 1.17.0.1 is available on CRAN now. Besides several bug fixes and small changes, it introduces more values in input of coords.
Here is an example:
library(pROC) data(aSAH) rocobj <- roc(aSAH$outcome, aSAH$s100b) coords(rocobj, x = seq(0, 1, .1), input="recall", ret="precision") # precision # 1 NaN # 2 1.0000000 # 3 1.0000000 # 4 0.8601399 # 5 0.6721311 # 6 0.6307692 # 7 0.6373057 # 8 0.4803347 # 9 0.4517906 # 10 0.3997833 # 11 0.3628319
Getting the update
The update his available on CRAN now. You can update your installation by simply typing:
install.packages("pROC")
Here is the full changelog:
1.17.0.1 (2020-01-07):
- Fix CRAN incoming checks as requested by CRAN.
1.17.0 (2020-12-29)
- Accept more values in
inputofcoords(issue #67). - Accept
kappafor thepower.roc.testof two ROC curves (issue #82). - The
inputargument tocoordsforsmooth.roccurves no longer has a default. - The
xargument tocoordsforsmooth.roccan now be set toall(also the default). - Fix bootstrap
roc.testandcovwithsmooth.roccurves. - The
ggrocfunction can now plotsmooth.roccurves (issue #86). - Remove warnings with
warnPartialMatchDollaroption (issue #87). - Make tests depending on vdiffr conditional (issue #88).
Xavier Robin
Published Wednesday, January 13, 2021 16:19 CET
Permalink: /blog/2021/01/13/proc-1.17.0.1
Tags:
pROC
Comments: 2
 pROC 1.16.1
pROC 1.16.1
pROC version 1.16.1 is a minor release that disables a timing-dependent test based on the microbenchmark package that can sometimes cause random failures on CRAN. This version contains no user-visible changes. Users don't need to install this update.
Xavier Robin
Published Tuesday, January 14, 2020 08:52 CET
Permalink: /blog/2020/01/14/proc-1.16.1
Tags:
pROC
Comments: 0
 pROC 1.16.0
pROC 1.16.0
pROC version 1.16.0 is available on CRAN now. Besides several bug fixes, the main change is the switch of the default value of the transpose argument to the coords function from TRUE to FALSE. As announced earlier, this is a backward incompatible change that will break any script that did not previously set the transpose argument and for now comes with a warning to make debugging easier. Scripts that set transpose explicitly are not unaffected.
New return values of coords and ci.coords
With transpose = FALSE, the coords returns a tidy data.frame suitable for use in pipelines:
data(aSAH) rocobj <- roc(aSAH$outcome, aSAH$s100b) coords(rocobj, c(0.05, 0.2, 0.5), transpose = FALSE) # threshold specificity sensitivity # 0.05 0.05 0.06944444 0.9756098 # 0.2 0.20 0.80555556 0.6341463 # 0.5 0.50 0.97222222 0.2926829
The function doesn't drop dimensions, so the result is always a data.frame, even if it has only one row and/or one column.
If speed is of utmost importance, you can get the results as a non-transposed matrix instead:
coords(rocobj, c(0.05, 0.2, 0.5), transpose = FALSE, as.matrix = TRUE) # threshold specificity sensitivity # [1,] 0.05 0.06944444 0.9756098 # [2,] 0.20 0.80555556 0.6341463 # [3,] 0.50 0.97222222 0.2926829
In some scenarios this can be a tiny bit faster, and is used internally in ci.coords.
Type help(coords_transpose) for additional information.
ci.coords
The ci.coords function now returns a list-like object:
ciobj <- ci.coords(rocobj, c(0.05, 0.2, 0.5)) ciobj$accuracy # 2.5% 50% 97.5% # 1 0.3628319 0.3982301 0.4424779 # 2 0.6637168 0.7433628 0.8141593 # 3 0.6725664 0.7256637 0.7787611
The print function prints a table with all the results, however this table is generated on the fly and not available directly.
ciobj # 95% CI (2000 stratified bootstrap replicates): # threshold sensitivity.low sensitivity.median sensitivity.high # 0.05 0.05 0.9268 0.9756 1.0000 # 0.2 0.20 0.4878 0.6341 0.7805 # 0.5 0.50 0.1707 0.2927 0.4390 # specificity.low specificity.median specificity.high accuracy.low # 0.05 0.01389 0.06944 0.1250 0.3628 # 0.2 0.70830 0.80560 0.8889 0.6637 # 0.5 0.93060 0.97220 1.0000 0.6726 # accuracy.median accuracy.high # 0.05 0.3982 0.4425 # 0.2 0.7434 0.8142 # 0.5 0.7257 0.7788
The following code snippet can be used to obtain all the information calculated by the function:
for (ret in attr(ciobj, "ret")) {
print(ciobj[[ret]])
}
# 2.5% 50% 97.5%
# 1 0.9268293 0.9756098 1.0000000
# 2 0.4878049 0.6341463 0.7804878
# 3 0.1707317 0.2926829 0.4390244
# 2.5% 50% 97.5%
# 1 0.01388889 0.06944444 0.1250000
# 2 0.70833333 0.80555556 0.8888889
# 3 0.93055556 0.97222222 1.0000000
# 2.5% 50% 97.5%
# 1 0.3628319 0.3982301 0.4424779
# 2 0.6637168 0.7433628 0.8141593
# 3 0.6725664 0.7256637 0.7787611
Getting the update
The update his available on CRAN now. You can update your installation by simply typing:
install.packages("pROC")
Here is the full changelog:
- BACKWARD INCOMPATIBLE CHANGE:
transposeargument tocoordsswitched toFALSEby default (issue #54). - BACKWARD INCOMPATIBLE CHANGE:
ci.coordsreturn value is now of list type and easier to use. - Fix one-sided DeLong test for curves with
direction=">"(issue #64). - Fix an error in
ci.coordsdue to expectedNAvalues in some coords (like "precision") (issue #65). - Ordrered predictors are converted to numeric in a more robust way (issue #63).
- Cleaned up
power.roc.testcode (issue #50). - Fix pairing with
roc.formulaand warn ifna.actionis not set to"na.pass"or"na.fail"(issue #68). - Fix
ci.coordsnot working withsmooth.roccurves.
Xavier Robin
Published Sunday, January 12, 2020 21:46 CET
Permalink: /blog/2020/01/12/proc-1.16.0
Tags:
pROC
Comments: 0
 pROC 1.15.3
pROC 1.15.3
A new version of pROC, 1.15.3, has been released and is now available on CRAN. It is a minor bugfix release. Versions 1.15.1 and 1.15.2 were rejected from CRAN.
Here is the full changelog:
- Fix
-Infthreshold in coords for curves withdirection = ">"(issue 60). - Keep list order in
ggroc(issue 58). - Fix erroneous error in
ci.coordswithret="threshold"(issue 57). - Restore lazy loading of the data and fix an
R CMD checkwarning "Variables with usage in documentation object 'aSAH' not in code". - Fix vdiffr unit tests with ggplot2 3.2.0 (issue 53).
Xavier Robin
Published Monday, July 22, 2019 09:07 CEST
Permalink: /blog/2019/07/22/proc-1.15.3
Tags:
pROC
Comments: 0
 pROC 1.15.0
pROC 1.15.0
The latest version of pROC, 1.15.0 has just been released. It features significant speed improvements, many bug fixes, new methods for use in dplyr pipelines, increased verbosity, and prepares the way for some backwards-incompatible changes upcoming in pROC 1.16.0.
Verbosity
Since its initial release, pROC has been detecting the levels of the positive and negative classes (cases and controls), as well as the direction of the comparison, that is whether values are higher in case or in control observations. Until now it has been doing so silently, but this has lead to several issues and misunderstandings in the past. In particular, because of the detection of direction, ROC curves in pROC will nearly always have an AUC higher than 0.5, which can at times hide problems with certain classifiers, or cause bias in resampling operations such as bootstrapping or cross-validation.
In order to increase transparency, pROC 1.15.0 now prints a message on the command line when it auto-detects one of these two arguments.
> roc(aSAH$outcome, aSAH$ndka)
Setting levels: control = Good, case = Poor
Setting direction: controls < cases
Call:
roc.default(response = aSAH$outcome, predictor = aSAH$ndka)
Data: aSAH$ndka in 72 controls (aSAH$outcome Good) < 41 cases (aSAH$outcome Poor).
Area under the curve: 0.612
If you run pROC repeatedly in loops, you may want to turn off these diagnostic messsages. The recommended way is to explicitly specify them explicitly:
roc(aSAH$outcome, aSAH$ndka, levels = c("Good", "Poor"), direction = "<")
Alternatively you can pass quiet = TRUE to the ROC function to silenty ignore them.
roc(aSAH$outcome, aSAH$ndka, quiet = TRUE)
As mentioned earlier this last option should be avoided when you are resampling, such as in bootstrap or cross-validation, as this could silently hide some biases due to changing directions.
Speed
Several bottlenecks have been removed, yielding significant speedups in the roc function with algorithm = 2 (see issue 44), as well as in the coords function which is now vectorized much more efficiently (see issue 52) and scales much better with the number of coordinates to calculate. With these improvements pROC is now as fast as other ROC R packages such as ROCR.
With Big Data becoming more and more prevalent, every speed up matters and making pROC faster has very high priority. If you think that a particular computation is abnormally slow, for instance with a particular combination of arguments, feel free to submit a bug report.
As a consequence, algorithm = 2 is now used by default for numeric predictors, and is automatically selected by the new algorithm = 6 meta algorithm. algorithm = 3 remains slightly faster with very low numbers of thresholds (below 50) and is still the default with ordered factor predictors.
Pipelines
The roc function can be used in pipelines, for instance with dplyr or magrittr. This is still a highly experimental feature and will change significantly in future versions (see issue 54 for instance). Here is an example of usage:
library(dplyr)
aSAH %>%
filter(gender == "Female") %>%
roc(outcome, s100b)
The roc.data.frame method supports both standard and non-standard evaluation (NSE), and the roc_ function supports standard evaluation only. By default it returns the roc object, which can then be piped to the coords function to extract coordinates that can be used in further pipelines
aSAH %>%
filter(gender == "Female") %>%
roc(outcome, s100b) %>%
coords(transpose=FALSE) %>%
filter(sensitivity > 0.6,
specificity > 0.6)
More details and use cases are available in the ?roc help page.
Transposing coordinates
Since the initial release of pROC, the coords function has been returning a matrix with thresholds in columns, and the coordinate variables in rows.
data(aSAH) rocobj <- roc(aSAH$outcome, aSAH$s100b) coords(rocobj, c(0.05, 0.2, 0.5)) # 0.05 0.2 0.5 # threshold 0.05000000 0.2000000 0.5000000 # specificity 0.06944444 0.8055556 0.9722222 # sensitivity 0.97560976 0.6341463 0.2926829
This format doesn't conform to the grammar of the tidyverse, outlined by Hadley Wickham in his Tidy Data 2014 paper, which has become prevalent in modern R language. In addition, the dropping of dimensions by default makes it difficult to guess what type of data coords is going to return.
coords(rocobj, "best") # threshold specificity sensitivity # 0.2050000 0.8055556 0.6341463 # A numeric vector
Although it is possible to pass drop = FALSE, the fact that it is not the default makes the behaviour unintuitive. In an upcoming version of pROC, this will be changed and coords will return a data.frame with the thresholds in rows and measurement in colums by default.
Changes in 1.15
- Addition of the
transposeargument. - Display a warning if
transposeis missing. Passtransposeexplicitly to silence the warning. - Deprecation of
as.list.
With transpose = FALSE, the output is a tidy data.frame suitable for use in pipelines:
coords(rocobj, c(0.05, 0.2, 0.5), transpose = FALSE) # threshold specificity sensitivity # 0.05 0.05 0.06944444 0.9756098 # 0.2 0.20 0.80555556 0.6341463 # 0.5 0.50 0.97222222 0.2926829
It is recommended that new developments set transpose = FALSE explicitly. Currently these changes are neutral to the API and do not affect functionality outside of a warning.
Upcoming backwards incompatible changes in future version (1.16)
The next version of pROC will change the default transpose to FALSE. This is a backward incompatible change that will break any script that did not previously set transpose and will initially come with a warning to make debugging easier. Scripts that set transpose explicitly will be unaffected.
Recommendations
If you are writing a script calling the coords function, set transpose = FALSE to silence the warning and make sure your script keeps running smoothly once the default transpose is changed to FALSE. It is also possible to set transpose = TRUE to keep the current behavior, however is likely to be deprecated in the long term, and ultimately dropped.
New coords return values
The coords function can now return two new values, "youden" and "closest.topleft". They can be returned regardless of whether input = "best" and of the value of the best.method argument, although they will not be re-calculated if possible. They follow the best.weights argument as expected. See issue 48 for more information.
Bug fixes
Several small bugs have been fixed in this version of pROC. Most of them were identified thanks to an increased unit test coverage. 65% of the code is now unit tested, up from 46% a year ago. The main weak points remain the testing of all bootstrapping and resampling operations. If you notice any unexpected or wrong behavior in those, or in any other function, feel free to submit a bug report.
Getting the update
The update his available on CRAN now. You can update your installation by simply typing:
install.packages("pROC")
Here is the full changelog:
rocnow prints messages when autodetectinglevelsanddirectionby default. Turn off withquiet = TRUEor set these values explicitly.- Speedup with
algorithm = 2(issue 44) and incoords(issue 52). - New
algorithm = 6(used by default) usesalgorithm = 2for numeric data, andalgorithm = 3for ordered vectors. - New
roc.data.framemethod androc_function for use in pipelines. coordscan now returns"youden"and"closest.topleft"values (issue 48).- New
transposeargument forcoords,TRUEby default (issue 54). - Use text instead of Tcl/Tk progress bar by default (issue 51).
- Fix
method = "density"smoothing when called directly fromroc(issue 49). - Renamed
rocargumentntosmooth.n. - Fixed 'are.paired' ignoring smoothing arguments of
roc2withreturn.paired.rocs. - New
retoption"all"incoords(issue 47) dropincoordsnow drops the dimension ofrettoo (issue 43)
Xavier Robin
Published Saturday, June 1, 2019 09:33 CEST
Permalink: /blog/2019/06/01/proc-1.15.0
Tags:
pROC
Comments: 0
 pROC 1.14.0
pROC 1.14.0
pROC 1.14.0 was released with many bug fixes and some new features.
Multiclass ROC
The multiclass.roc function can now take a multivariate input with columns corresponding to scores of the different classes. The columns must be named with the corresponding class labels. Thanks Matthias Döring for the contribution.
Let's see how to use it in practice with the iris dataset. Let's first split the dataset into a training and test sets:
data(iris) iris.sample <- sample(1:150) iris.train <- iris[iris.sample[1:75],] iris.test <- iris[iris.sample[76:150],]
We'll use the nnet package to generate some predictions. We use the type="prob" to the predict function to get class probabilities.
library("nnet")
mn.net <- nnet::multinom(Species ~ ., iris.train)
iris.predictions <- predict(mn.net, newdata=iris.test, type="prob")
head(iris.predictions)
setosa versicolor virginica 63 2.877502e-21 1.000000e+00 6.647660e-19 134 1.726936e-27 9.999346e-01 6.543642e-05 150 1.074627e-28 7.914019e-03 9.920860e-01 120 6.687744e-34 9.986586e-01 1.341419e-03 6 1.000000e+00 1.845491e-24 6.590050e-72 129 4.094873e-45 1.779882e-15 1.000000e+00
Notice the column names, identical to the class labels. Now we can use the multiclass.roc function directly:
multiclass.roc(iris.test$Species, iris.predictions)
Many modelling functions have similar interfaces, where the output of predict can be changed with an extra argument. Check their documentation to find out how to get the required data.
Multiple aesthetics for ggroc
It is now possible to pass several aesthetics to ggroc. So for instance you can map a curve to both colour and linetype:
roc.list <- roc(outcome ~ s100b + ndka + wfns, data = aSAH)
ggroc(roc.list, aes=c("linetype", "color"))
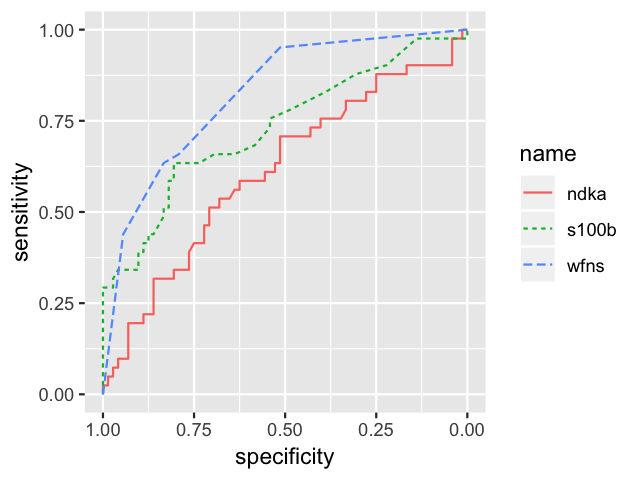 Mapping 3 ROC curves to 2 aesthetics with ggroc.
Mapping 3 ROC curves to 2 aesthetics with ggroc.
Getting the update
The update his available on CRAN now. You can update your installation by simply typing:
install.packages("pROC")
Here is the full changelog:
- The
multiclass.rocfunction now accepts multivariate decision values (code contributed by Matthias Döring). ggrocsupports multiple aesthetics.- Make ggplot2 dependency optional.
- Suggested packages can be installed interactively when required.
- Passing both
casesandcontrolsorresponseandpredictorarguments is now an error. - Many small bug fixes.
Xavier Robin
Published Wednesday, March 13, 2019 10:22 CET
Permalink: /blog/2019/03/13/proc-1.14.0
Tags:
pROC
Comments: 0
 Search
Search Tags
Tags Recent posts
Recent posts Calendar
Calendar Syndication
Syndication